Applies to reactions in which all reacting species are in the same phase.
Example: 3 H2 (g) + N2 (g) ↔ 2 NH3 (g)
2. Heterogeneous equilibria
Applies to reactions in which the reacting species are in the different phase.
Example: CaCO3 (s) ↔ CaO (s) + CO2 (g)
3. The expression of equilibrium constant
(a) Equilibrium constant in terms of concentration (Kc)For reactions involved aqueous solutions and gases.
(b) Equilibrium constant in terms of partial pressure (Kp)
For reactions involved gases only.
Example: 3 H2 (g) + N2 (g) ↔ 2 NH3 (g)
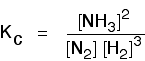
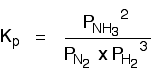
Note: The concentration of pure solid and liquid (such as water) are excluded in the equilibrium constant expression (Kc and Kp) since their concentrations are remained constant in their pure form.

4. The relationship between Kc and Kp
Consider a general reaction: aA (g) + bB (g) ↔ cC (g) + dD (g)
 ...... (1)
...... (1) ...... (2)
...... (2)Assume that the gases behave ideally,
From ideal gas equation,
PV = nRT
For gas A, PAeV = nART
 where PAe = equilibrium partial pressure for gas A
where PAe = equilibrium partial pressure for gas A PAe = [A]e RT ...... (3)
By subsituting the partial pressure for each gases into equation (2),


Kp = Kc (RT)(c+d)-(a+b)
where Δn = n(gaseous product) - n(gaseous reactant)
R = 0.08206 L atm mol-1 K-1
Example: 3 H2 (g) + N2 (g) ↔ 2 NH3 (g)
Δn = n(gaseous product) - n(gaseous reactant)
= 2 - 4
= -2
5. Important characteristic of equilibrium constant
Consider the reaction,

For a reverse reaction,

For a reaction with different stoichiometry coefficient (different number of moles),

Summary:

6. Calculating Kc, Kp or the quantities of species present at equilibrium
(a) The equilibrium constants can be calculated if the quantities of species present at equilibrium (such as concentration or partial pressure) are given.
Example:
For a reaction,
3 H2 (g) + N2 (g) ↔ 2 NH3 (g)
An amount of 2.00 mol H2, 1.00 mol N2 and 2.00 mol NH3 was found in a 1.0 L flask at equilibrium. Calculate Kc.
=
(b) The equilibrium constants can be used to calculate the quantities of species present at equilibrium, such as equilibrium concentration or partial pressure. It can be done by constructing an ICE (Initial-Change-Equilibrium) table.
Example:
In a reaction, 1.000 M H2 and 2.000 M I2 were placed in a vessel and allowed to react at a constant temperature. Given that Kc is 50.5, calculate the equilibrium concentration for H2, I2 and HI.

4x2 = 50.5(2.000 - 3.000x + x2)
46.5x2 - 151.5x + 101.0 = 0
x = 0.935 or 2.323 (not acceptable)
x = 0.935
(Note: By substituting 2.323 into the expression for equilibrium concentrations, the equilibrium concentration for H2 and I2 is found to be negative, which is not chemically meaningful. Thus, the value of 2.323 is not acceptable)
[H2] = 1.000 - 0.935 = 0.065 M
[I2] = 2.000 - 0.935 = 1.065 M
[HI] = 2(0.935) = 1.87 M
7. Degree of dissociation (α)
For a decomposition reaction (a molecule is broken down into smaller molecules),
CaCO3 (s) ↔ CaO (s) + CO2 (g)
α = change in concentration (or partial pressure) / initial concentration (or partial pressure)
8. Prediciting the direction of reaction
The reaction quotient (Q) is the mass action expression at any stage of the reaction.
Consider a general reaction: aA (g) + bB (g) ↔ cC (g) + dD (g)

The reaction quotient (Q) is used to detemine the direction of a reaction will proceed to reach equilibrium.
If
Q = K, the system is at equilibrium.
Q > K, the system is not at equilibrium, the reaction will shift to left.
Q < K, the system is not at equilibrium, the reaction will shift to right.

Example:
The Kc is 51 at 448oC for the following reaction:
H2 (g) + I2 (g) ↔ 2 HI (g)
Predict in which direction the reaction will proceed to reach equilibrium if 5.0x10-2 mol H2, 1.5x10-2 mol I2 and 1.0x10-2 mol HI were placed in a 1.0 L flask at the same temperature.
Qc < Kc, the equilibrium position will shift to right.
No comments:
Post a Comment